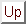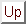
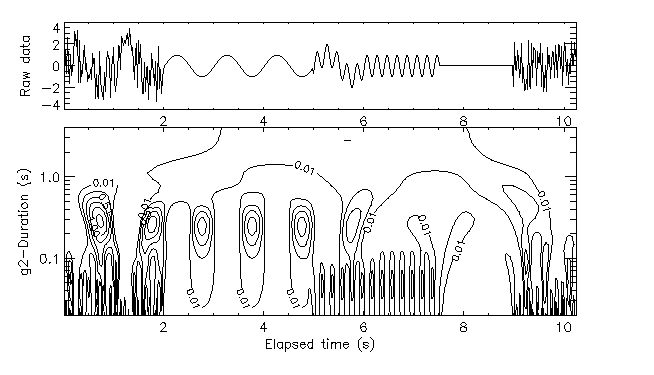
As pointed out earlier, if the data are periodic, Fourier analysis is best and there is no need for wavelet transforms. Thus, it is time we show the result of wavelet analysis on artificial data with controled non-periodicity to illustrate some of the salient features.
First, we show the graph of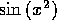 
with its Mexican-hat wavelet
transform (Fig 12).
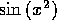showing the gradual shift to
shorter durations.
The wavelet map shows the gradual shift of local maxima and minima toward shorter durations, as expected. Next, a sine wave was modulated both in intensity and in frequency. The corresponding shifts in duration and energy are shown on the next figure (Fig. 13).
Finally, a composite signal was generated by superposition of excerpts of sine waves at different frequencies and random noise. Only positive contour lines of a Mexican-hat wavelet map (Fig. 14) are shown for clarity.
