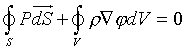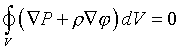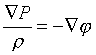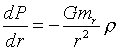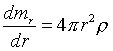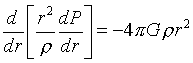Гидростатическое равновесие в звездах

Пожалуй важнейшим условием равновесия в звездах можно считать условие механического равновесия, то есть равенства сил, действующих на любой, произвольно выделенный объем в звезде. Хотя в абсолютном смысле это условие не может справедливым - практически любая звезда эволюционирует в той или иной мере, то есть меняет свой радиус, а значит существует сила, выполняющая эту работу. Однако характерное время такого измененяи в большинстве случаев столь велико (млрд. лет), что с любой разумной точностью условие равновесия следует считать выполненным. (Исключения составляют "взрывные" стадии эволюции звезды, которые весьма интересны, но очень далеки от понимания).

В классической теории эволюции принимаются в расчет только две силы, равновесие между которыми и называют гидростатическим. Первая - это давление на выделенный объем со стороны других элементов газа (то есть термодинамическое давление самой плазмы), а вторая - сила гравитационного притяжения элементов объема со стороны других элементов, составляющих звезду. Очевидно, что именно эти силы рассматриваются в гидростатике, единственным отличием является то, что поле сил тяжести в гидростатике обычно предполагается внешним.

Для получения необходимого уравнения просто приравняем все силы давления P, действующие каждый, достаточно маленький чтобы считаться плоским элемент поверхности dS, окружающей выделенный объем V, и сумму сил притяжения каждого элемента массы dm, то есть

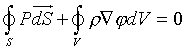
Теперь интеграл по поверхности следует заменить на интеграл по объему. Такая замена выполняется с помощью теоремы Гаусса-Остроградского, смысл которой состоит в возможности разбить наш объем на множество маленких эелементиков "удобной" формы, например цилиндров (необязательно круговых) с осью, направленной вдоль градиента давления СP. Тогда интеграл по поверхности может быть вычислен как интеграл по объему, ограниченному этой поверхностью, но уже от градиента давления (для маленького цилидра это не трудно доказать). Наше условие переходит в

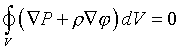
Но поскольку мы никак не ограничивали выбор нашего объема, по которому ведется интегрирование, то единственный способ гарантировать выполнение этого условия - потребовать, чтобы подынтегральное выражение было равно нулю в любой точке звезды. Тогда получается дифференциальное уравнение, выражающее гидростатическое равновесие звезды.

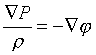
Данное уравнение справедливо для любого случая гидростатического равновесия, включая, например, неизотропное давление (нужно только правильно понимать операцию градиента от тензора давления). Однако в случае звезд, логично воспользоваться предположением о сферической симметрии звезды, тем более, что пока не видно сил, которые могли бы нарушать такую симметрию. В этом случае существует выражение для гравитационного потенциала j (и его градиента) через массу слоев m_r, заключенных в сфере под рассматриваемой точкой - см. уравнение Пуассона. Кроме того, предположение о сферической симметрии позволяет записать дифференциальные уравнения для производных по радиусу, поскольку все остальные производные, входящие в градиент, просто равны нулю. В результате, уравнение принимает вид

с добавлением соответствующего уравнения, определяющего величину m_r

Легко понять, что из этих двух уравнений можно исключить одну неизвестную, например m_r. Правда, порядок уравнения при этом повысится до второго, а неизвестных останется все равно две.

(к этому уравнению проще всего прийти сразу из векторного условия равновесия, применяя оператор градиента и используя уравнение Пуассона

Нужно только не забыть, что под внешним градиентом в левой части стоит векторная функция, то есть он означает дивергенцию - отсюда и множитель r² в записи уравнения в сферических координатах).

Векторное уравнение второго порядка для известного давления как функции плотности.

В.Батурин