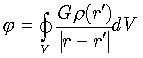
| предыдущая |
следующая
|
Для описания сил самогравитации в звездах можно использовать гравитационный потенциал j. По смыслу, потенциал соответствует работе, которую нужно совершить, чтобы разнести два взаимодействующих (притягивающихся) элемента массы на бесконечное расстояние. Поскольку на интересует притяжение выбранного элемента со стороны всех других элементов массы, то общий потенциал примем как сумму потенциалов элементарных взаимодействий, т.е.
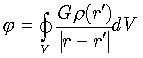
Теорема Пуассона утверждает (благодаря чему так называется итоговое уравнение), что применение оператора D (Лапласиана) к данному интегралу даст в результате просто
нужное нам уравнение Пуассона для гравитационного потенциала. Как мы видели при выводе уравнения гидростатического равновесия, полученное выражение можно непосредственно использовать для вывода уравнения второго порядка, включающего как условие равновесия, так и уравнение для потенциала.
С другой стороны, в сферически-симметричной звезде, с введением ускорения силы тяжести g=-Сj, уравнение Пуассона можно проинтегрировать один раз, получив
здесь mr - масса, заключенная внутри сферы радиуса r. Хорошо известным свойством гравитационного потенциала является отсутствие силы притяжения со стороны внешних сферических симметричных слоев.
В.Батурин
| предыдущая |
следующая
|