Сохранение энергии в звездах

Вывод соотношений, выражающих энергетический баланс в звездах, почти дословно повторяет рассуждения о гидростатическом равновесии - выделяем произвольный объем, окруженный поверхностью. Через поверхность проходит поток тепла F_Q, а внутри могут существовать источники энергии (ядерной, или гравитационной), удельную мощность (эрг в сек на грамм) которых обозначим за e. Тогда снова выписываем интегральное соотношение баланса, а затем переходим к дифференциальной (локальной) форме

Вычисление каждого из членов в правой части является независимой задачей - при построении модели звезды мы должны считать, что энерговыделение известно как функция температуры и плотности. Если речь о выделении энергии в ядерных реакциях, то эта задача ядерной физики, решение которой весьма трудоемко. С точки зрения сохранения энергии в звездах, следует заметить, что существует энергия нейтрино, потоко которой обычно считают свободно (без потерь) выходящим за пределы звезды. Таким образом, он не может быть включен в локальное уравнение энергетического баланса. Иногда это записывают в виде e_N-e_n.

Что касается гравитационного члена, то речь идет о выделении или поглощении энергии благодаря сжатию или расширению звезды в процессе эволюции. В несколько обощенной форме этот член записывают в виде

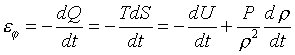
Эти слагаемые выражают потери энергию на работу по расширению или сжатию вещества, и аккомулирование (или освобождение) энергии во внутренней энергии плазмы. Отметим только, что использование записи через производную энтропии справедливо лишь при "термодинамически обратимых процессах", то есть строго говоря, не верно для областей, где происходят изменения химического состава (благодаря ядерным реакциям или диффузии).

Для расчетов строения сферически симметричных звезд этого уравнение записывают ввиде

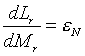
где L_{r - светимость сферы радиуса r, а Mr - масса внутри этой сферы.}

В.Батурин