| предыдущая |
вверх
|
следующая
|
Изложим качественно некоторые представления статистической физики на примере идеального газа. Хотя большинство предположений могут и не использоваться при анализе термодинамики идеального газа, но во-первых, эти предположения актуальны при рассмотрении более сложных случаев, а во-вторых, использовое общего статистического описания позволяет всецело определить идеальный газ, включая его энтропию, и все необходимые распределения (по скоростям или флюктуации средних величин).
Существуют два основных метода для описания распределений в статистической физике. Одно, это распределение Гиббса (или большое каноническое распределение) и второе, это распределение Максвелла-Больцмана (или микроканоническое распределение). Несмотря на то, что распределение Гиббса в некотором смысле более общее, наглядно представлять легче второй тип, то есть микроканоническое распределение. Поэтому мы начнем со второго.
Прежде чем перейти к описанию распределеннй, отметим общую черту (точнее, основной принцип) для обоих типов. Этот принцип состоит в том, что вероятность системы (или объекта) находиться в состоянии i (что это за объекты и состояния - зависит от типа распределения) пропорциональна e-Ei/kT, где Ei - энергия этого состояния.
Несколько в шуточной форме можно сказать, что ситуация подобна случайному размещению книг на стелажах сложной формы. Каждое место, куда книга может быть поставлена, это состояние i, а высота полки, на которой мы ищем книгу - это ее энергия. Тогда для каждой книги можно сопоставить "температуру", характеризующую то, как часто эту книгу брали и ставили на место. А вероятность найти книгу на высоких полках (при умеренных "температурах") существенно меньше, чем на самых высоких. При этом форма стелажа и количество мест на каждой полке может быть очень разным - именно это характеризует конкретную систему.
Вернемся к микроканоническому распредtлению и опишем "стелажи". В начале, не будем вспоминать о квантовых эффектах, так сказать, чисто классическое описание. В основе лежит представление о фазовом пространстве или его еще называют m- пространством для одной частицы. Если рассматривать частицу из идеального газа, ее фазовое пространство 6-мерное, и состоит из 3-х координатных и 3-х импульсных осей. Частица, в общем случае, может занимать любое положение в этом пространстве, ограниченное по координатным осям размерами системы. Поскольку мы не предполагаем никаких внешних сил (сил тяжести, магнитных полей и т.п.), то энергия частицы не зависит от положения в пространстве, и вероятности всех доступных положений в пространсвенных координатах одинаковы. Тем самым мы способны нарисовать оси импульсов из фазового пространства, и оперировать с ними в дальнейшем. Энергия частицы определяется квадратом импульса и массой, то есть в пространстве импульсов все сферические "стелажи" имеют одинаковые энергии (находятся на одинаковой "высоте"). Однако объемы этих стелажей не одинаковы - они пропорциональны объемам шаровых слоев со средним радиусом p. Объем этого слоя очевидно равен 4pp2dp. Все положения внутри этого слоя равновероятны, так что если мы интересуемся распредление по импульсам (тоже, что по энергиям), то получим, что вероятность w(p) равна
В этой формуле начальная константа имеет смысл нормировки плотности вероятности, то есть находится из условия, тw(p)dp=1. Эту формулу легко переписать в виде распределения скоростей частиц, то есть
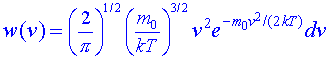
хорошо известное распределение Максвелла для скоростей частиц в идеальном газе. Легко понять, что можно использовать это полученное распределение для вывода макроскопического давления, в механическом смысле. Едиственное, что для этого нужно, это убедиться, что средняя энергия частиц E=тw(E)dE остается равной 3kT/2.
Упражнение. Покажите, что наиболее вероятная скорость частиц равна (2kT/m0)1/2, средняя скорость равна (8kT/pm0)1/2, а среднеквадратичная скорость равна (3kT/m0)1/2.
Вернемся к константе нормировки в распределении импульсов (2pm0kT)-1/2. Эта величина смысл среднего импульса частиц при рассматриваемом распределении.
| предыдущая |
в
начало
|
следующая
|