| предыдущая |
следующая
|
Идея лучистого переноса энергии состоит в том, что фотоны излучаются в более горячих областях звезды и поглощаются в более холодных, перенося таким образом энергию. Эффективность такого переноса, среди всего прочего, зависит от градиента температуры и от способности фотонов свободно путешествовать от одной области звезды до другой. Чаще всего в звездах фотон может пройти всего 1 см без того, чтобы испытать взаимодействие с веществом, поэтому лишь микроскопическая разница температур существует на конечных точках этого переноса. Так как излучательная способность вещества пропорциональна четвертой степени температуры, можно ожидать, что скорость переноса энергии будет пропорциональна градиенту четвертой степени температуры. Кроме того, эффективность переноса будет зависеть от непрозрачности вещества по отношению к конкретным фотонам, то есть какой путь они могут проходить без поглощения. Так же ясно, что градиент температуры является необходимым условием существования переноса тепла, поскольку при его отсутствии излучение изотропно и тепло не переносится.
Чтобы получить математическое выражение для градиента температуры как функции переносимого потока, воспользуемся качественными соображениями, ведущими, однако, к правильному результату. Рассмотрим поле свободных фотонов, то есть в то время, пока они не претерпели поглощение или другой взаимодействие с веществом. Если обозначить плотность фотонов как n, то поток излучения будет даваться формулой
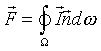
(интеграл берется по всем направлениям). В то же время импульс, переносимый через площадку dS дается выраженим
Таким образом, для поля излучения как такового можно записать вполне строго закон сохранения импульса в виде
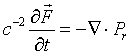
Далее, допустим некоторые "нестрогости" вывода. Мы "усредним" данное уравнением по времени жизни фотона tg , уравнение ввиде
В действительности, это уравнение дает то, что нам нужно. Можно заменить время жизни фотона на длину свободного пробега, деленную на скорость, и получить в более привычном виде
или выразить поток через светимость сферы радиуса r, а давление излучения через температуру, так же как длину свободного пробега через непрозрачность. Тогда уравнение примет совсем привычный вид
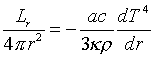
В.Батурин
| предыдущая |
следующая
|